计算机系统课程上讲到的 IEEE 754 32位浮点数一些规则细节的个人理解与解释。 老师在课上已经把各个细节都大致讲过了,这篇文章是给课后对这些细节还感兴趣的同学,做补充解释和扩展。
这篇文章不会采用晦涩的引用或者证明,而是尝试让同学能直观理解 IEEE 754 的一些设计选择。
2021-03-31: 最近有比较多的同学看到了这篇文章,这篇文章的本意是回答几个课上遇到的具体问题,而对 IEEE 754 本身的介绍方面的完整性和系统性可能不及其他资料,建议配合其他资料阅读。
重温课上的例子
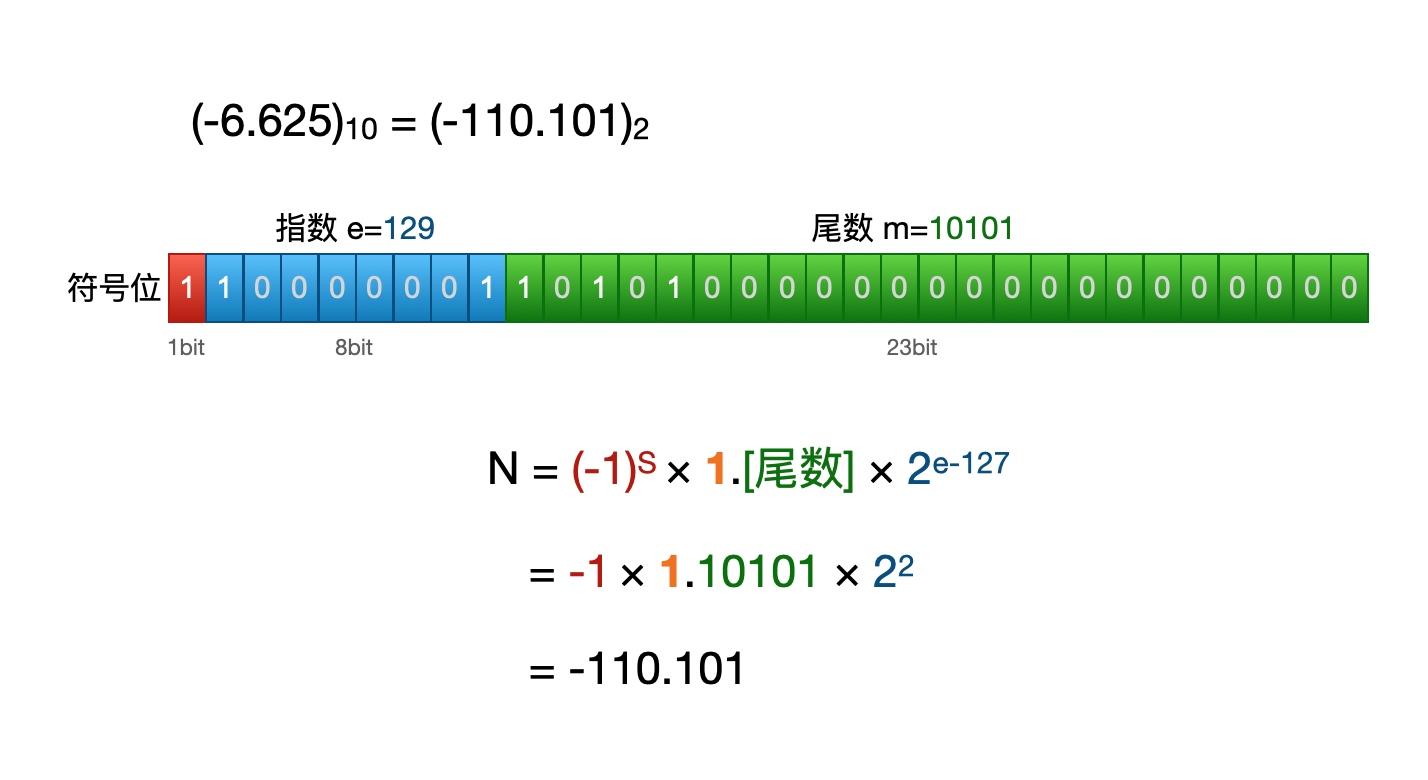
课上老师讲过,现代的计算机是以 IEEE 754 的标准来存储浮点数的,以 32 位浮点数 6.625 为例子:
-6.625 = -(4 + 2 + 1/2 + 1/8),一位一位对应过来,二进制表示就是 -110.101,那么使用浮点数表示 6.625 的话,内存中实际存储的比特位是这个样子的:
其实可以观察到,浮点数的存储,本质上就是二进制的科学记数法:由一个有效数字(绿色部分),乘上一个数量级(蓝色部分)来表示一个小数。
为什么有效数字的整数部分要规定为 1 ?
根据公式可以观察到,尾数前面的整数部分,IEEE 754 规定(当 1 ≤ e ≤ 254 的时候)固定是 1。
有同学问,为什么这里非得是 1 呢?假设整数部分是 0 可不可以呢?
其实 0 也是可以的,但是这样其实就浪费了一个位的精度了。
我们知道浮点数在内存中的表示,其实就是二进制的科学记数法。我们先考虑我们所熟悉的十进制,十进制下科学记数法为了达到最高效地表示数字的目的,是规定不允许有效数字的整数部分是 0 的,如果整数部分是 0 的话,就通过改变数量级指数来调整,使得整数部分变成 1 到 9 之间的整数。
1
0.365 * 10^5 => 3.65 * 10^4
二进制的科学记数法也是一样的,我们为了高效简介的表达,也像十进制的科学记数法一样,规定有效数字的整数部分不能是 0(因为前导 0 是无效数字,并不能提供任何信息)。
也就是说,例如
111010
它的二进制科学记数法是1.11010 * 2^5
而不是0.111010 * 2^6,因为这种表示不是最高效简介的表示方法
但是专家们很快发现:既然都规定了科学记数法有效数字的整数部分不能是 0 ,因为二进制只有 0 和 1 两种数字,那整数部分不就只剩下 1 这一种可能性了吗?
于是通过规定整数部分不为 0 ,加上二进制本身的性质,我们得到一个结论:二进制数的科学记数法中,有效数字的整数部分永远是 1。
知道这个结论以后,我们会发现,我们其实就没必要花内存去存有效数字(例如 1.11010)开头的这个 1 了,因为我们已经知道个位肯定是 1 了,只存有效数字的小数部分(.11010)就行了。
例如
1.11010 * 2^5,已知二进制科学记数法有效数字必然是1.开头的
所以只需要花内存去存小数点后面的尾数11010就足够了
这就是为什么在二进制浮点数中 仅用 23 个 bit 就能表示 24 位的精度,这多出来的 1 个 “免费的精度” 是二进制的特性所共同提供的。
(ps. 如果是 10 进制的话,因为有效数字的整数部分有 1 ~ 9 九种情况,就不能像二进制这样省略掉不存第一位)
我们也可以做一个小实验,我们还是以 -110.101 作为例子,看一下如果假设有效数字个位规定为 0,会有什么效果:
规定 1 为整数部分(IEEE 754 的做法,与开头的例子相同)
规定 0 为整数部分(我们自己假想的做法,注意对比 N 公式的变化)
(注意对比两种方案的尾数)
我们会发现,我们按照 IEEE 754 专家们的规矩去存储的话,需要存储的尾数部分是 10101,但是如果按照我们假设个位是 0 去存储的话,我们的尾数就变成 110101了。
这也印证了我们前面提到的,有效数字整数部分如果为 0 的话,这种表示不是最高效的。
也就是对于同样的数据,假设有效数字整数部分规定是 0 的话,我们的尾数要多浪费一个位,去存储这一个我们明明知道的 1。
为什么指数 e 要用移码表示?而不是带符号位的原码或补码?
同学提到,为什么指数要用移码表示?也就是为什么要把它加上 127 去存储?不是无论哪一种存储方式,表示的范围不都是一样的吗?
答案是为了简化浮点数的运算和大小比较。对于浮点数,我们进行大小比较的时候,其实就是比较两个科学记数法表示的数字,所以第一步肯定是先比较他们的数量级。 如果数量级都不一样大,那就没有必要去比较有效数字部分的具体大小了,因为数量级大的表示的数字肯定更大。
浮点数中的数量级大小由指数 e 决定,思考一下,假设现在指数不用移码,而是采用带符号位的原码表示的话,需要考虑什么?
首先我们要检查符号位,要看符号是不是一样的,如果不一样的话,正数要比负数大。而符号位同正呢?同负呢?同正的话是不是就是绝对值大的数比较大?同负的话是不是绝对值小的数比较大?那就得实现两套比较逻辑,对应两种不同的情况。
首先要把符号关系搞清楚(++,+-,-+,--),然后,再按符号关系执行多套不同的逻辑,这样实现起来 CPU 电路会很复杂。
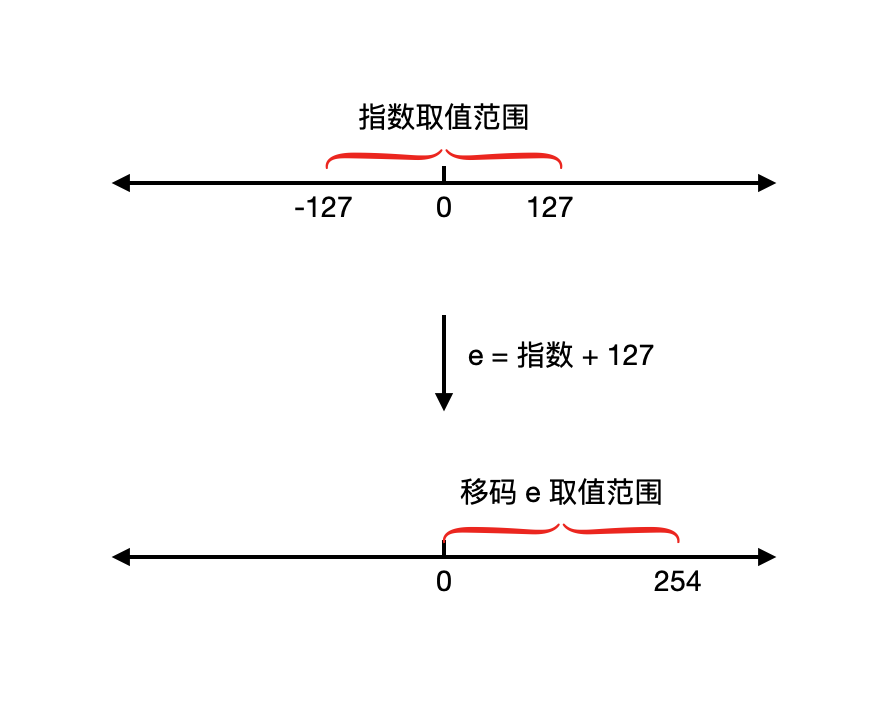
所以当时设计 IEEE 754 的专家为了保持简洁,就干脆不要符号位了,直接规定我们把指数加上 127 再存储。加上 127 就把指数的取值范围 “移” 到正数上来了。
这样比较指数大小(数量级大小)的时候就不用考虑异号或者同号了,因为都是正数,采用同一套比较电路直接比较就行了,而正数之间的比较电路是很简单的,所以也就简化了 CPU 的设计。
为什么是 +127 而不是 +128?
8bit 有符号整数的范围是-128 ~ 127,但是将整个指数的范围移动到整数上,只需要加 127 就可以了,不用加 128
因为在 IEEE 754 中,指数 = -128被规定保留为表示特殊情况了(具体用途是用来表示很小的数字,称为 Subnormal number)
实际上指数 = 128也被规定保留为表示特殊情况了(NaN / Infinity)
我们能够取到的指数范围只剩下-127 ~ 127
所以不需要偏移 128,只需要偏移 127 就足够了